Accelerating Matrix Multiplication using FPGAs

Introduction

Matrix multiplication is among the most foundational of algorithms in scientific computing, used in fields ranging from computational fluid dynamics to artificial intelligence. Naturally, building high-performance implementations is of great concern to engineers. The massive parallelism provided by GPUs has heightened interest in the possibilities of hardware acceleration, leading some firms to develop custom hardware intended solely for matrix operations, such as Google’s TPU. In this post, I will demonstrate a hardware matrix multiplier implementation targeting AMD’s Zynq 7000 SoC.

Credit

This blog post was inspired by Georgia Tech Professor Callie Hao’s ECE 8893 graduate course, Parallel Programming for FPGAs. I use the reference implementation as a starting point for my optimization. The course materials are publicly available on GitHub.

For the sake of consistency, both the reference implementation and my optimized implementation multiply a $100 \times 150$ matrix by a $150 \times 200$ matrix. Both matrices contain 16-bit integers.

Zynq SoC

AMD’s Zynq 7000 contains an ARM processor that interfaces with a programmable logic device. This SoC is compatible with Pynq, a set of Python libraries that enable programs to interface with custom hardware, akin to how NVIDIA’s CUDA libraries provide a convenient API for GPU kernel developers.

High-Level Synthesis (HLS)

HLS tools, like AMD’s Vitis HLS suite, enable hardware engineers to define algorithms in high-level languages that are translated to RTL implementations. HLS eliminates some of the burden of implementing performance optimizations directly in HDLs.

Accelerator Design

Reference Implementation

The provided implementation contains three main steps:

Load the operand matrices from system DRAM to local BRAM
Use a nested loop to compute the matrix product, storing the result in BRAM
Copy the result matrix from BRAM to DRAM

This approach is sensible, but there are a few major issues with the implementation:

For very large matrices, it is impractical to copy them fully from system memory to constrained local memory
The opportunities provided by the FPGA’s concurrency are left untapped; if the dependencies between data are minimal, it is simple to express intent for concurrent execution
Only one AXI bundle is in use, limiting the memory bandwidth of the kernel

My design remedies these pitfalls, achieving a four times performance increase.

Reference Synthesis Performance Report:

Notice that the reference implementation needs an estimated 3.3M cycles for one matrix multiplication. My optimized implementation only needs 788K cycles, but the speedup comes at a cost: Significantly higher resource usage.

Optimized Implementation

My design offers the following benefits over the reference design:

My design leverages block matrix multiplication, as outlined in Kastner et al. (141), significantly increasing scalability. Because block multiplication operates on subsets of the larger matrix operands, it is ideal for streaming use cases, enabling my design to scale to larger matrices that might not fit entirely in local memory
- I use a BLOCK_SIZE of 4, meaning that each block multiplication involves a $4 \times 150$ matrix and a $150 \times 4$ matrix, resulting in a $4 \times 4$ matrix. For optimal performance, BLOCK_SIZE should be a power of 2. The performance of my implementation doubled when I increased the BLOCK_SIZE from 2 to 4
The loops in my code are pipelined with a target initiation interval of 1. That is, one iteration of each pipelined loop completes every clock cycle, improving hardware utilization (e.g., memory transfers are not blocked as computation progresses)
I allocate three AXI bundles for communication, improving kernel throughput. Additionally, using separate AXI bundles enables me to decorate the CallBlockMatmul loop with the DATAFLOW pragma
The three function calls inside the CallBlockMatmul loop are part of a dataflow. Dataflows are like pipelines, enabling the loop to iterate as function calls continue
I partition the BRAM buffers, delivering a slight performance improvement. Partitioning enables further data parallelism
- According to AMD’s documentation, the array_partition pragma cannot be used with the DRAM buffers, since my design interfaces with host DRAM through m_axi interfaces

My design provides a starting point for multiple other projects and improvements:

As I alluded to earlier, my design is well-suited for streaming. I would like to test my code against larger matrices
Rather than using two sets of doubly-nested loops to transfer data from DRAM to BRAM, it is possible to use one nested loop with some simple branching logic
My design uses block array partitioning, but others have had success with cyclic partitioning. I would like to explore other partitioning schemes further

Hardware Testing

Vivado Workflow

AMD’s Vivado tool allows hardware engineers to integrate custom IP cores produced by Vitis HLS with other components in their design. Vivado automatically configures the AXI bus infrastructure, enabling seamless communication between the matrix multiplication IP core and the ARM processor.

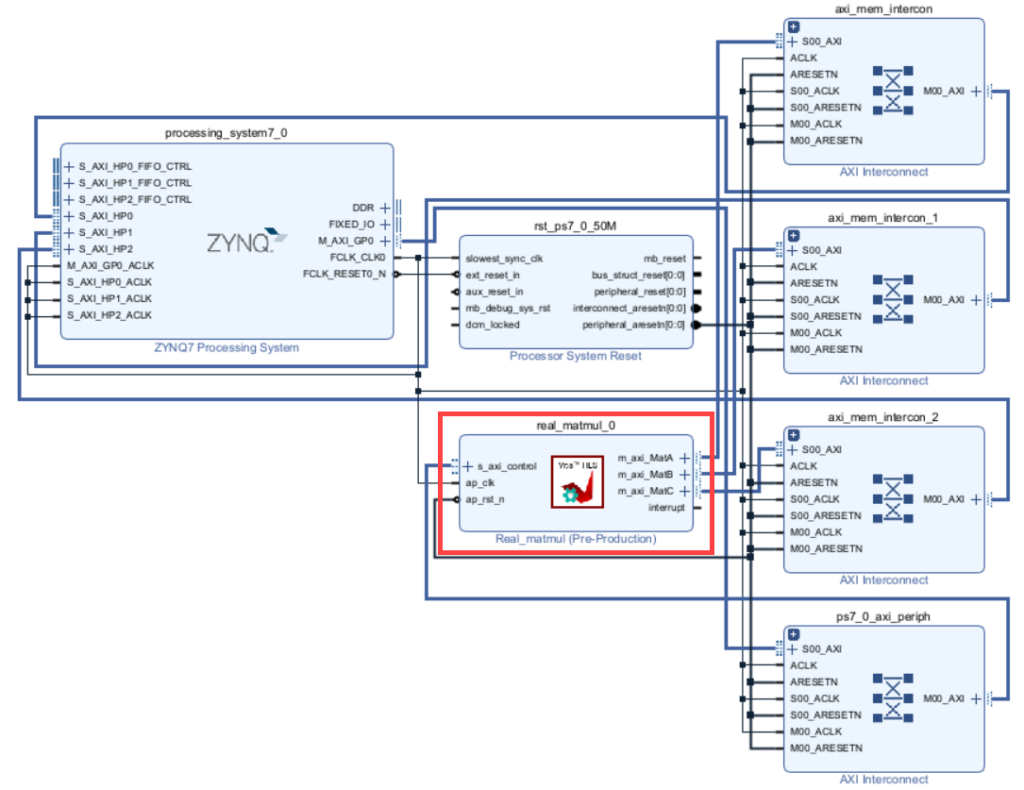
*The matrix multiplication IP core is highlighted in the full implementation. Notice the three AXI bundles, `MatA`, `MatB`, and `MatC`.*

After generating an HDL wrapper for my design, Vivado synthesizes the HDL and produces a bitstream. The Zynq SoC only needs an automatically-generated hardware handoff file and a bitstream to leverage a new design.

*Layout of LUTs, BRAMs, and queues, among other components in my design, after Vivado generates a bitstream.*

Development Board

I use the Pynq library to flash my design onto the SoC and test it using randomly-initialized Numpy arrays. I recommend the popular TUL PYNQ Z2 development board, which contains GPIO headers compatible with common microcontrollers. After flashing the board’s SD card with TUL’s Linux image, I navigate to its Jupyter interface in my browser. The following Python script validates my design.